# 线性神经网络

# 线性回归

• 线性回归是对 n 维输入的加权，外加偏差，通常用于预测，方程形式：

$$y = w_1x_1 + w_2x_2 + ... + b$$

• 通常使用 MSE 损失去衡量预测的精确性，即预测值$\hat{y}$ 和真实值 y 的均方差：

$$L_{MSE} = \frac{1}{2}||\hat{y} - y||^2$$

• 线性回归一般有显式解，显式解是损失导数为 0 的点。
• 线性回归可以看做是单层神经网络，$w_i$ 实际上是唯一的一层神经元的权重。

pytorch 实现线性回归很简单。线性回归可以被看成是一层神经网络，因此可以用全连接层实现：

net = nn.Linear(2, 1)

Linear 第一个参数是输入数据形状的最后一个维度，比如输入数据 features.shape 是 [4,2]，那么 Linear 第一个参数就是 2。通常输入数据的最后一个维度是数据的特征，2 代表输入数据有两个维度的特征，如买房数据有房价和占地面积两个维度的特征。第二个参数就是输出数据形状的最后一个维度。

# 基础优化算法概览

# 梯度下降

基本思想是，对一组初始化的参数，反复迭代训练，按照下面的公式进行参数更新，使得最小化损失函数：

$$w_t = w_{t-1} - \alpha \frac{\partial Loss}{\partial w_{t-1}}$$

$\alpha$ 是学习率。学习率是一个很重要的超参，设置太大会导致模型无法收敛，设置太小会导致收敛过慢。

# 小批量梯度下降

在整个训练集上进行求梯度、求导会很慢。我们可以随机采样 b 个样本，计算损失来近似整个训练集上的损失。这个 b 就是 batch_size （批量大小），不能设置太大，太大导致内存占用过高，设置太小又无法充分发挥硬件潜力。

# 基本深度学习训练流程

以线性回归为例，假设我们要建立一个这样的模型：

$$y = 2x_1 -3.4x_2 + 4.2$$

事先导入需要用的包：

import numpy as np

import torch

from torch.utils import data

from d2l import torch as d2l

人工生成数据：

def synthetic_data(w, b, num_examples):

    """生成y=Xw+b+噪声"""

    X = torch.normal(0, 1, (num_examples, len(w)))

    y = torch.matmul(X, w) + b

    y += torch.normal(0, 0.01, y.shape)

    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])

true_b = 4.2

features, labels = synthetic_data(true_w, true_b, 1000)	# 生成 1k 个样本。

数据案例：

print('features:', features[0],'\nlabel:', labels[0])

# 返回

# features: tensor([-0.3679, -1.8471]) 

# label: tensor([9.7361])

features 是样本的特征，本质是一个二维数组，长度为 1000，而 label 是样本的预测真实值。这里每个样本有两个特征，对每个特征单独分析，都会发现其与 label 存在线性关系：

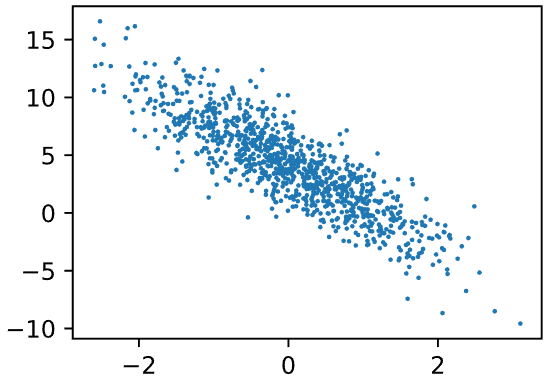
读取数据集的函数，返回一个 dataloader：

def load_array(data_arrays, batch_size, is_train=True):

    """构造一个PyTorch数据迭代器"""

    dataset = data.TensorDataset(*data_arrays)

    return data.DataLoader(dataset, batch_size, shuffle=is_train)

数据情况示例：

batch_size = 10

data_iter = load_array((features, labels), batch_size)

next(iter(data_iter))

# 结果分别是 features 和 labels：

# [tensor([[ 0.1554, -0.2034],

#          [-0.2140,  1.0352],

#          [-0.4209,  0.0428],

#          [ 0.1887,  0.6141],

#          [ 0.4987, -0.2314],

#          [ 0.0653,  1.6406],

#          [-1.1881,  0.2900],

#          [-0.2824,  0.5910],

#          [ 0.9963, -0.1816],

#          [-1.6830, -1.3963]]),

#  tensor([[ 5.2116],

#          [ 0.2479],

#          [ 3.2188],

#          [ 2.4845],

#          [ 5.9884],

#          [-1.2453],

#          [ 0.8441],

#          [ 1.6217],

#          [ 6.8072],

#         [ 5.5692]])]

我们的目的就是使用这 1000 个样本，训练出一个线性回归模型，也就是求出 w 和 b，以最大化预测的精度，即给定一个样本特征，能够尽可能估计出其对应 label 的值。

初始化线性回归模型的参数，然后在训练过程中，这些参数会被学习、调整。定义模型和损失函数，并初始化模型参数：

# nn 是神经网络的缩写

from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

loss = nn.MSELoss()

net[0].weight.data.normal_(0, 0.01)

net[0].bias.data.fill_(0)

正如前面所说的，对整个数据集进行梯度求导会相当费时，所以通常采用小批量梯度下降 ——SGD。

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

这样就可以开始训练了：

num_epochs = 3

for epoch in range(num_epochs):

    for X, y in data_iter:

        l = loss(net(X) ,y)

        trainer.zero_grad()

        l.backward()

        trainer.step()

    l = loss(net(features), labels)

    print(f'epoch {epoch + 1}, loss {l:f}')

# 训练过程举例：

# epoch 1, loss 0.043705

# epoch 2, loss 0.000172

# epoch 3, loss 0.000047

# 回归、分类与独热编码

回归可以用于预测的问题，比如预测房屋被售出价格，或者棒球队可能获得的胜场数，又或者患者住院的天数，回归的输出是一个连续的数值。

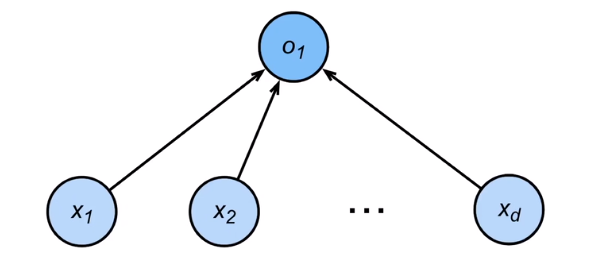
分类则更倾向于问 “哪一个”。比如，某个电子邮件是否属于垃圾邮件，某张图像是驴、狗、猫还是鸡。分类问题通常是多个输出，输出 i 是模型预测输入为第 i 类的置信度。

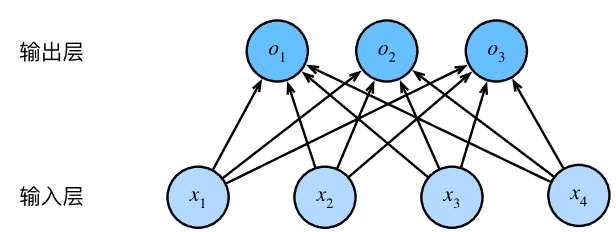
独热编码能够很好地应用到分类问题上，比如有三个类别：{狗，猫，鸡}。在计算机中，可以用 (1,0,0) 代表狗，用 (0,1,0) 代表猫，用 (0,0,1) 代表鸡。也就是说，用向量表示标签，分量和类别一样多，都是 3。类别对应的分量设置为 1，其他所有分量不是这个类别的设置为 0，这就是独热编码。

# Softmax 运算与全连接层

softmax 运算将数据转换为 [0,1] 区间的数值，可以理解为一种标准化，数值可以认为是概率。比如，一个长度为 3 的向量经过 softmax 操作后，3 个数值都会被转换为 0 到 1 的区间值，并且相加和为 1。

softmax 公式如下：

$$softmax(x) = \frac{exp(x_i)}{\sum_{k}^{len(x)}exp(x_k)}$$

全连接层无处不在，前面提到全连接层可以很方便地通过 nn.Linear 实现。但是全连接层也不是没有缺点，参数量冗余是问题。对于任何具有 d 个输入和 q 个输出的全连接层（对应在最后一个维度上，输入和输出的特征数分别为 d 和 q），参数量开销为 O (dq)。

后续会提到用 Dropout 方法处理这个问题。

# 经典损失函数

# L1 损失

# L2 损失

# Huber 鲁棒损失

# 交叉熵损失

# 信息论基础

# 多层感知机

# 多层感知机理论

前面提到的线性回归是一种线性神经网络，这样的网络存在一种假设：输入和输出是线性相关的。这种假设下，任何输入的特征增大都会导致模型的输出增大或减小。但很多时候，输入和输出并非是线性相关的。比如一张图像，增加某个位置的像素的强度值能否总是增大其分类为狗的概率？

我们可以在网络中加入一个或多个隐藏层来突破线性模型的限制，使其能处理更普遍的函数关系类型。这种架构称为多层感知机（ multilayer perceptron, MLP ），这是堆叠许多全连接层的神经网络。

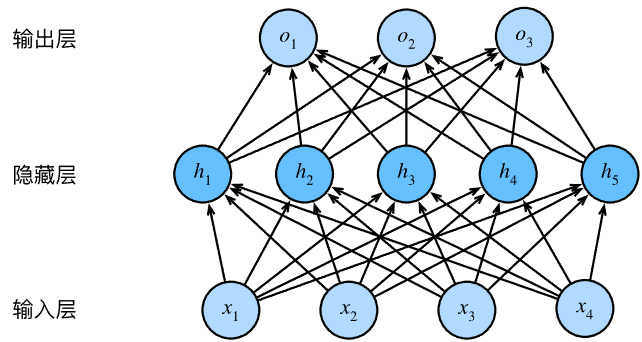
每两个层都是全连接的，每个输入都会影响隐藏层中的每个神经元，而隐藏层中的每个神经元又会影响输出层中的每个神经元。

如果输入$X \in \mathbb{R}^{n \times d}$，n 是小样本数，d 是输入特征。对于隐藏层有权重$W_1 \in \mathbb{R}^{d \times h}$、偏置$b_1 \in \mathbb{R}^{1 \times h}$，输出层也有权重$W_2 \in \mathbb{R}^{h \times q}$ 和偏置$b_2 \in \mathbb{R}^{1 \times q}$。其中，h 通常是这个隐藏层的隐藏单元数，q 是输出的输出特征，如果要分类为 10 类，q 就是 10。因此多层感知机（单个隐藏层）的数学表达式可以表示为，O 是输出，H 称为隐藏表征（ hidden representation ）：

$$H = XW_1 + b_1 \\ O = HW_2 + b_2$$

# 激活函数

没有激活函数的多层感知机相当于线性神经网络。观察上面的表达式，隐藏单元由输入的仿射变换给出，而输出也只是隐藏单元的仿射函数。仿射函数的仿射函数还是仿射函数，可以如下证明上面的多层感知机等价于单层模型：

$$O = (XW_1 + b_1)W_2 + b_2 = XW_1W_2 + b_1W_2 + b_2 = XW + b$$

这是因为，之前说到的线性回归模型已经可以表示任何仿射函数。通过合并，多层感知机退化为单层的线性回归模型。为了发挥多层架构的潜力，可以在仿射变换后应用非线性的激活函数（ activation function ），即：

$$H = \sigma(XW_1 + b_1) \\ O = \sigma(HW_2 + b_2)$$

这样，多层感知机避免了线性计算退化为单层的线性模型的风险。通过隐藏层中的神经元，多层感知机可以捕获输入之间复杂的相互作用，这些神经元依赖每个输入的值。如果给定足够的神经元和正确的权重，我们就可以对任意函数进行建模，尽管实际应用中学习该函数是很困难的。

# ReLU 函数

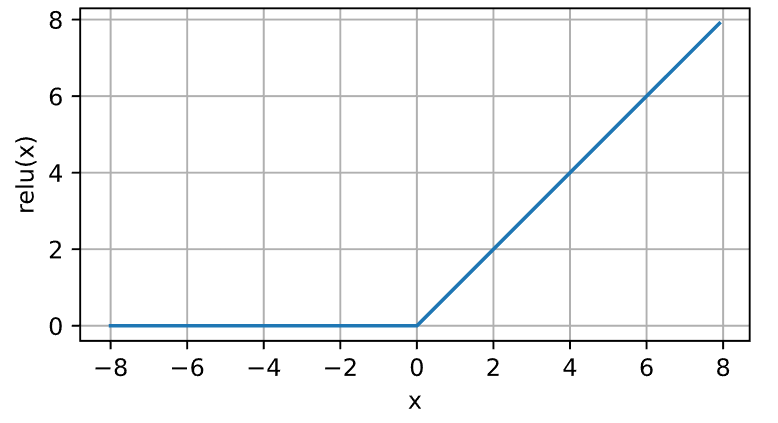
最受欢迎的激活函数：修正线性单元（ rectified linear unit, ReLU ）。数学表达式为：

$$ReLU(x) = max(x, 0)$$

ReLU 函数通过将相应的激活值设为 0，仅保留正元素并丢弃所有负元素。当输入值精确为 0 试， ReLU 函数不可导。 ReLU 函数求导很方便，优化表现好，并一定程度上缓解了以往神经网络的梯度消失问题。代码实现和函数曲线图如下：

y = torch.relu(x)

# sigmoid 函数

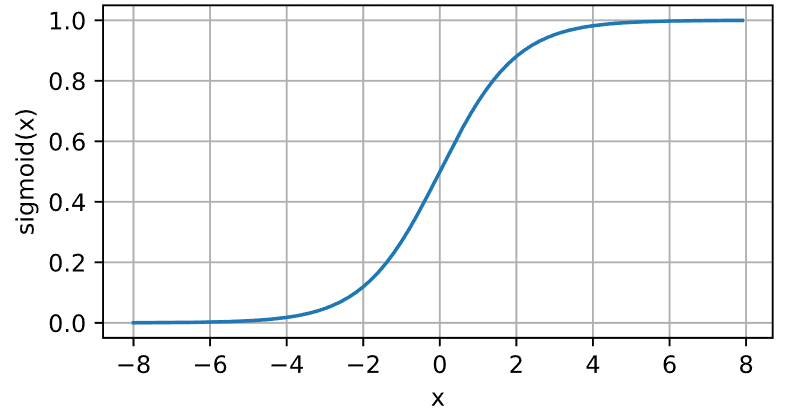
对于一个定义在$\mathbb{R}$ 的输入， sigmoid 激活函数将输入变换到 (0,1) 区间。数学表达式为：

$$sigmoid(x) = \frac{1}{1+exp(-x)}$$

这是一个平滑的、可微的阈值单元的近似函数。sigmoid 常被用做输出层的激活函数，这个时候，它输出二元分类的概率，因此 sigmoid 可以看作是 softmax 的一个特例。但是，隐藏层中的激活函数还是不选择 sigmoid，因为 ReLU 更合适。当输入接近 0 时，sigmoid 函数接近线性变换。代码实现和函数曲线图如下：

y = torch.sigmoid(x)

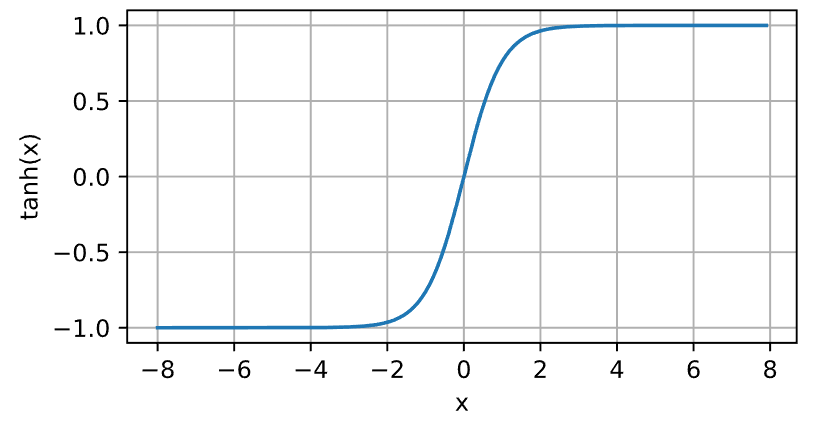
# Tanh 函数

Tanh （双曲正切）函数也是将输入压缩转换到区间 (-1,1) 上。函数公式如下：

$$tanh(x) = \frac{1 - exp(-2x)}{1+exp(-2x)}$$

输入在 0 附近时，它和 sigmoid 函数一样，接近线性变换。代码实现和函数曲线图如下：

y = torch.tanh(x)