:::info
学习自李宏毅与蘑菇书。蘑菇书链接:蘑菇书EasyRL (datawhalechina.github.io)
搭配李宏毅的强化学习课程使用最佳。
这篇博文内容结合了自己的理解,不可避免地会存在不当,欢迎指正。
:::
组成
智能体Actor、环境Environment与奖励Reward。在后面的内容中,你都可以将智能体理解为玩游戏的机器人,将环境理解为游戏主机,奖励理解为机器人玩游戏干掉怪兽得到的分数。
策略梯度算法(Policy gradient Algorithm)
智能体通常作为Actor,在 ++策略++ 不断调整与指引下使得其在环境重获取到最大的奖励。策略在具体的实现上,现代强化学习通常用网络替代之。在前面的比喻中,你可以将策略理解为机器人取得高分的方法和手段。
符号定义:
| 符号 | 释义 |
|---|---|
| $t$ | 同一时间下的某个状态 |
| $T$ | 某个轨迹下的所有状态数 |
| $a_t$ | 某个状态下智能体的动作 |
| $s_t$ | 某个状态下的环境 |
| $\theta$ | 智能体的策略模型参数 |
| $r_t$ | 某个状态下智能体采取动作后的奖励 |
| $\tau_i$ | 某次轨迹:所有状态的环境与动作的组合。$\tau=\{s_1,a_1,s_2,a_2,…s_t,a_t\}$ |
| $p$ | 概率 |
| $R$ | 总奖励 |
关键公式推导
给定智能体Actor的参数$\theta$,可以计算轨迹$\tau$的发生的概率:
$p_{\theta}(a_1|s_1)$是策略里面的网络参数$\theta$决定的、观察到环境$s_1$后采取的动作概率。因此策略网络的输出是一个分布,是智能体采取动作的概率分布。$p(s_2|s_1,a_1)$是环境根据前一个环境的状态和智能体的动作给出的下一个环境状态,通常是环境内部的规则决定。
一个轨迹$\tau$会在某个时刻终止,其内部的每一个$s_t$和$a_t$的组合均能够产生对应的奖励$r_t$。所以,所有的组合能够得到一个关于这个轨迹的总奖励$R(\tau)$。
我们的目的就是要调整策略网络的参数$\theta$使得总奖励$R(\tau)$越大越好。因此,$R(\tau)$是一个随机的变量,我们可以计算$R(\tau)$:
当策略参数$\theta$给定,那么在这组参数上一定有一个关于轨迹的分布$p_{\theta}(\tau)$,智能体的多次尝试都是一个轨迹。对于所有的轨迹$\tau_i$,存在总奖励$\overline{R}_{\theta}$的期望值为:
为了让 ++期望奖励++ 越大越好,要进行 ++梯度上升++ 。所以要计算期望奖励关于策略参数$\theta$的梯度:
因此有:
但是在实际上,我们是无法直接和准确地求期望值$\mathbb{E}_{\tau \sim p_{\theta}(\tau)}[R(\tau)\nabla logp_{\theta}(\tau)]$的。但是我们可以通过采样N个$\tau$,然后计算$R(\tau)\nabla logp_{\theta}(\tau)$的N个和,来近似地得到这个期望:
得到最后一行的原因,是因为$\nabla log p_{\theta}(\tau^n)$可以被展开:
因为,$p(s_1)$和$p(s_{t+1}|s_t,a_t)$来自环境,与智能体的策略参数$\theta$无关,因此第一项和第三项为0,原式化简:
训练思路
现在整理一下思路。在给出一个初始策略参数$\theta$的情况下,经过训练,我们要得到一个不错的策略参数$\theta$,使得智能体在多个轨迹下得到的总奖励$\overline{R}_{\theta}$最大化。如何优化这个$\theta$呢?我们可以通过梯度上升法优化这个$\theta$,使得当$s_t$状态下执行$a_t$导致$R(\tau)$增大时增加在$s_t$下执行$a_t$的概率,反之减小这个概率:
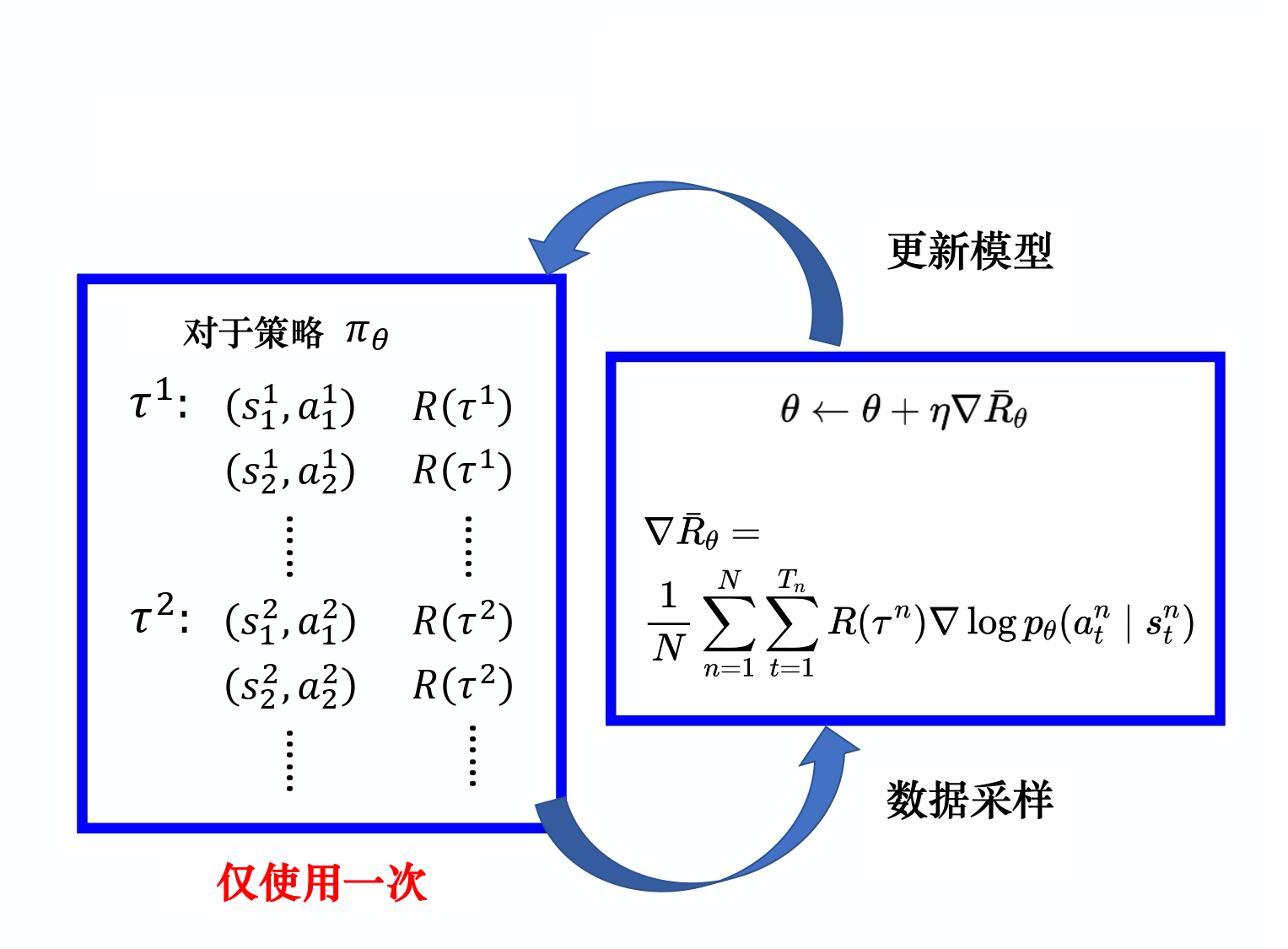
根据公式1.4和公式1.5,我们知道优化$\theta$的关键在于求出$\nabla \overline{R}_{\theta}$,与$\nabla \overline{R}_{\theta}$有关的是$s_t^n$、$a_t^n$和$\tau^n$。所以我们要采集这些数据:
$\tau$的采集量是人为设定的,采集完一次后,会获得多组$\tau$的数据,然后使用公式1.4和公式1.5一次性更新模型:
直观理解
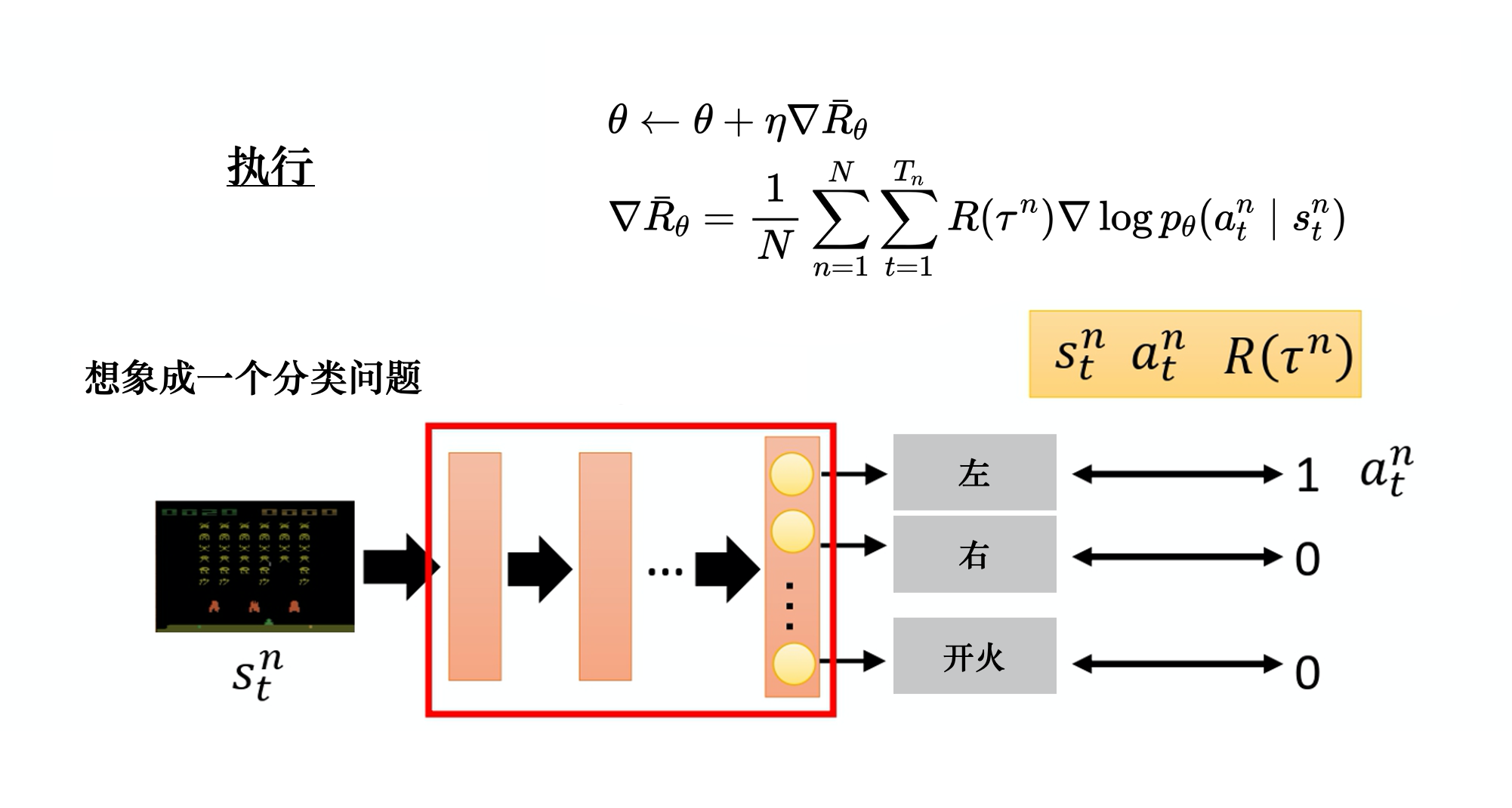
如何直观理解公式1.4?既然我们要通过求出$\nabla \overline{R}_{\theta}$来得到$\theta$的更新值,就不得不依赖反向传播得到梯度。你可以想象这样一个场景:智能体在玩一个游戏,控制一个飞机射击外星人,它的策略$\theta$是智能体内部的网络NN(Neural Network),在游戏过程中保持不变(游戏过程就是在采样若干组轨迹的s,a,R()对),智能体看到场景$s$,送给策略网络NN计算出要做的动作$a$的概率。如,向左移动的概率,向右移动的概率,开火的概率,所以这本质上是一个分类问题。
通常在训练过程中,我们需要智能体根据当前场景做出的动作是人为指定的,也就是说对于某个轨迹$\tau$的一个特定的$s$有个Ground-Truth,这个Ground-Truth就是在这个特定场景应该做出的动作$a$。比如,在某个场景$s_t$下,我们想要智能体向左,于是标签就是[1, 0, 0]。智能体将$s_t$作为策略网络$\theta$的输入,估计出向左的概率要尽可能接近1,即$p_{\theta}(a_t|s_t)$要尽可能接近1。
所以,在采样过程中,大量的$s_t^n$计算出大量的$p_{\theta}(a_t|s_t)$,那么根据每个$s_t$的标签,就能够计算一个交叉熵损失(cross entropy loss),最小化交叉熵损失就是在最大化似然:
所以,在训练过程中,最小化交叉熵损失,实际上在最大化某个轨迹的预测值的和。观察上面的式子,有没有发现在最小化损失,实际上在最大化$\nabla \overline{R}_{\theta}$。
在计算出损失后,通过反向传播,可以直接计算出$\nabla \overline{R}_{\theta}$的值,因此就能更新参数$\theta$了。